太陽活動の変動はどのような影響を及ぼすのか③~・太陽活動と景気循環との関係・~
景気循環とは、生産や消費などの経済活動が盛んになる好況とそれらが衰える不況とが交互に発生する周期的変動のことです。
経済学の主流派は、景気循環を純粋に経済学的に説明しようとしますが、景気循環を駆動しているのは、経済外的な要因、すなわち太陽活動の変動ではないのかという説が19世紀から存在していました。
今回は、この説を紹介しつつ、太陽活動の変動と景気循環との間に相関性があるかどうかを見てみたいと思います。
『太陽活動の変動はどのような影響を及ぼすのか』より引用します。
3.1. 太陽活動とジュグラー循環との関係
ジュグラー循環(Juglar cycle)とは、フランスの経済学者、ジョゼフ・クレマン・ジュグラー(Joseph Clément Juglar, 1819年 – 1905年)がその存在を主張した約7-11年で繰り返される景気拡大と縮小のサイクルである。このサイクルを太陽黒点数の変動で最初に説明しようとしたのは、イギリスの経済学者、ウィリアム・スタンリー・ジェヴォンズ(William Stanley Jevons, 1835年 – 1882年)である。ジェヴォンズよりも前に、イギリスの天文学者、フレデリック・ウィリアム・ハーシェル(Frederick William Herschel, 1738年 – 1822年)は、太陽黒点数と小麦の価格が連動することを指摘していた。ジェヴォンズは、それを承けて、農作物の価格の変動がジュグラー循環をもたらすと考えたのだ。
ジェヴォンズは、1878年の論文で、東インド会社がインドに輸出する商品の価格が、1710-11年、1721-22年、1731-32年と、10年おきにピークに達していることに注目した。以下の太陽黒点数の変動グラフを見てもわかる通り、これらは極大期から極小期に向けて、太陽黒点数が減少する時期に相当する。
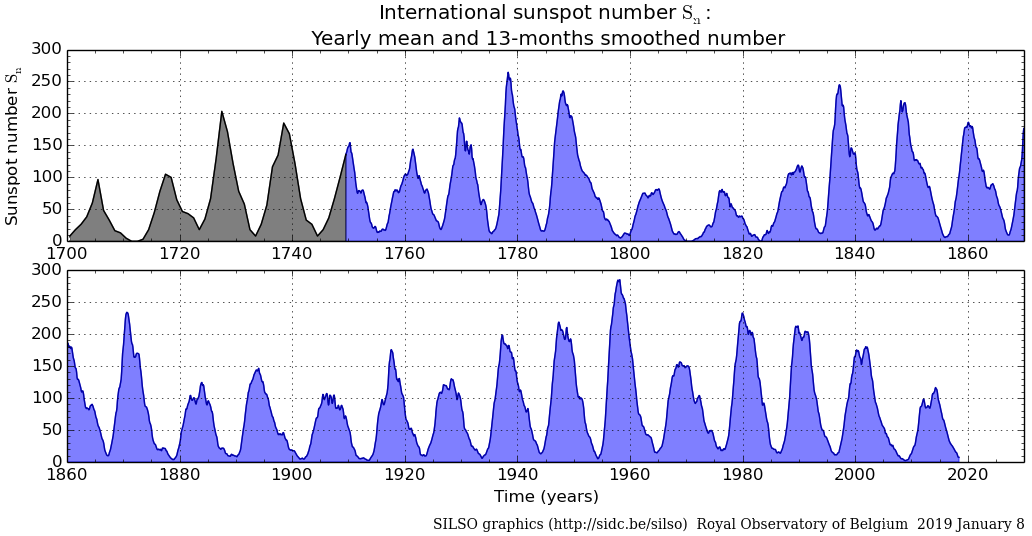
ジェヴォンズは、1879年の論文では、デリーの小麦粉の価格が、1763年、1773年、1783年、1792年、1803年、1826年にピークに達し、かつその時期に商業危機が起きていることに注目している。1826年を除けば、やはり、極大期から極小期に向けての時期に位置する。図を見てもわかる通り、1790年から1830年にかけてのダルトン極小期(Dalton Minimum)は太陽活動が長期にわたって低迷しており、規則性が失われている。デリーの小麦粉の価格は、1812年、1820年にも小さなピークに達しているので、ほぼ十年おきに極大期から極小期に向けての時期に価格が高騰するという規則性は維持されているが、商業危機は、1810年と1815年に起きており、対応していない。それでも、極小期に向けての時期に商品価格が高騰し、商業危機が起きやすくなるという傾向はあると言える。
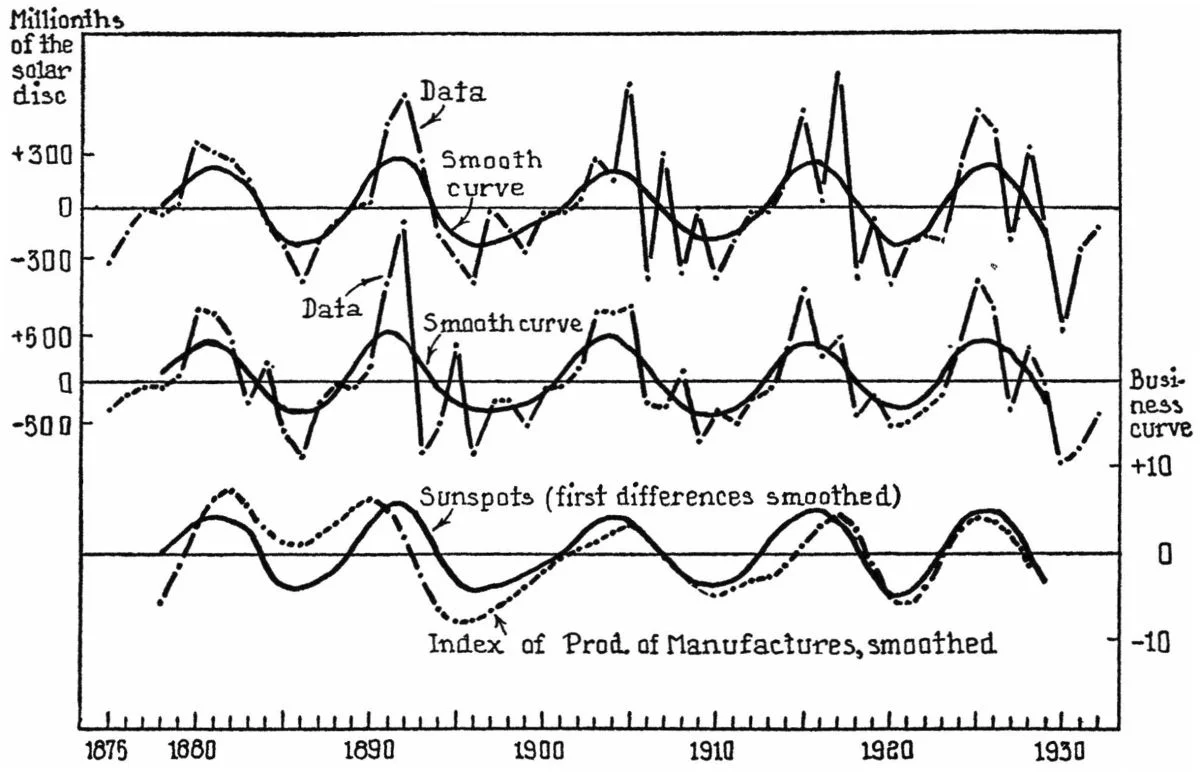
ジェヴォンズは、太陽活動が農業を通じて景気に影響を与えると考えたが、農作物の価格の高騰や暴落が景気を左右するという因果関係は逆ではないのかと疑うこともできる。すなわち、景気がよくなることで商品価格が高騰し、商業危機が起きることで商品価格が暴落するというように考えることもできるのである。1934年に、カルロス・ガルシア=マタ(Carlos Garcia-Mata)とフェリックス・シャフナー(Felix Shaffner)は、米国において太陽活動の変動と工業生産高の変動との間には相関性があるが、農業生産高(重量ベース)との間にはないことから、太陽活動の変動は、農業を媒介とせずに、直接工業に影響を与えているという仮説を提示した。この論文では、1875年から1931年までの期間にわたる、太陽活動と米国における製造業の総生産量と関係を示したグラフ(図16)を掲載している。一番上の実線グラフは、太陽活動の指標の加重移動平均で、その下の実線グラフは、農業と鉱業を除く製造業の総生産量の加重移動平均である。一番下の両者の重ね合わせを見れば、連動していることがよくわかる。
太陽活動の変動は、気候を変えることで農業に影響を与えるはずなのに、なぜ農業生産高(重量ベース)との間には相関性がないのか。世界各国の太陽活動と小麦の生産高の相関性を調べた論文によると、相関性が正の国もあれば、負の国もあり、米国のように相関性がない国もある。それはおそらく、太陽活動の変動が気候を変えるのに1年から4年のラグがあり、地域によってどれだけ遅れるかが違うために、11年周期のような短い周期では、広域的にはっきりした相関性が現れないのだろう。
もしも太陽活動が、農業を媒介とせずに直接製造業に影響を与えるとするなら、それはどのようなメカニズムによって起こるのか。ガルシア=マタとシャフナーは、景気循環を人間の心理で説明するアーサー・セシル・ピグー(Arthur Cecil Pigou, 1877年 – 1959年)の学説を引用しつつ、「太陽活動の変動が人間の心理的反応に直接、あるいは何らかの地上のメカニズムを通して影響を与えると仮定する必要がある」と言っている。
既に確認したとおり、太陽活動が活発になると、磁気嵐が激しくなり、それが脳波に摂動効果をもたらす。すると人々は冷静な判断力を失い、投機が過熱して好景気になる。太陽活動が不活発になると、磁気嵐も治まり、人々は冷静な判断力を取り戻し、投機バブルが崩壊する。こういう説明が考えられる。1924年に、ソ連の科学者、アレクサンドル・チジェフスキー(Алекса́ндр Чиже́вский, 1897年 – 1964年)は、ロシア革命をはじめとするヨーロッパの主要な革命が太陽黒点数の極大期に起きていることを発見した。革命の熱狂は、バブルの熱狂と同様に、磁気嵐が吹き荒れ、人々が冷静な判断ができない時に、起きやすくなるということである。
これ以外に可視光が投資家心理に与える影響も原因として加えることができる。太陽定数は、極大期においてわずかではあるが増加する。また、スベンスマルクの原理が成り立つ気候レジームにおいては、太陽活動の活発化は晴天の日を増加させる。1982年から1997年までの26カ国における朝の日差しと株式市場インデックスのリターンとの関係を調べた研究によると、日光は株価の収益と強い相関があることがわかった。晴れの日の方が、そうでない時よりも株価は上がりやすくなるということだ。
また、時間とともに日照時間が短くなる秋から冬にかけての季節には、季節性情動障害(Seasonal Affective Disorder=SAD)が発症しやすく、投資家たちも鬱になりやすくなる。このため、高緯度地域の市場では、株価の収益は低下しやすい。SAD効果と名付けられたこの現象は、季節が逆になる南北両半球で確認されることから、偶然ではないと考えられている。夏(特に7月)に「サマー・ラリー」で上昇した株価が秋(特に9月)になると下落しやすくなるという米国の株式市場のアノマリーは、通常タックス・ロス・セリング(節税対策)のためと説明されることが多いが、それに加えて、SAD効果で説明することもできる。そして、一年よりももっと長い周期、すなわちシュワーベ周期においても、雲量が増えて、日照時間が短くなりがちな太陽活動の低迷期に投資が減速して不況になりやすいという説明も可能になる。
もちろん、投資家の心理に影響を与える要因は他にもたくさんある。政府や中央銀行の政策変更もそうだ。ガルシア=マタとシャフナーが調べたのは、レッセ・フェール(自由放任)の経済政策が採られていた1875年から1931年までの時期の米国の経済である。政治的要因が投資家の心理に与えるケースは比較的少なかった。しかし、1929年末に世界恐慌が起きてから今日に至るまで、米国は、財政政策または金融政策(またはその両方)を通じて市場経済に積極的に介入するようになった。はたして、1931年以降も、ガルシア=マタとシャフナーが見出したような明確な対応関係はあるのだろうか。
そこで、太陽活動と経済の関係を調べた最近の研究成果を見てみよう。物理学者で経営コンサルタントのセオドア・モディス(Theodore Modis, 1943年 – )は、2007年に出版した論文「太陽黒点、GDP、株式市場」で、GDPや株価の長期的トレンドとの偏差が、太陽活動の変動の影響であるかどうかを調べた。以下の図は、1920年から2007年にかけての時期における米国GDPの11年移動平均線との偏差と太陽黒点数の変動とを重ね合わせたものである。

矢印で示された経済成長率のピークと太陽活動のシュワーベ周期のピークは対応しているようにも見えるが、1875年から1931年までの時期ほど明確な相関性はない。やはり政府や中央銀行による積極的な景気対策が、相関性を攪乱しているのだろう。
灰色のグラフの1930年代前半に見られる落ち込みは、世界恐慌によるものだ。その後、ニューディールによってやや持ち直すが、すぐに失速した。本格的に回復が始まるのは、1939年の第二次世界大戦開戦以降である。第二次世界大戦は、世界恐慌で生まれたデフレから脱却するための公共事業であり、ルーズベルト大統領にとっては、ニューディールの延長であった。この大規模な財政政策のおかげで、この時期は、経済成長率のピークと太陽活動のシュワーベ周期のピークが完全にずれている。1950年から1953年にかけて行われた朝鮮戦争、1965年から1973年にかけて米国が本格介入したベトナム戦争の時期にも、戦争ケインズ主義によって人為的に作り出されたと考えられる経済成長率のピークが見られる。これら時期においても、経済成長率と太陽活動の連動は、変則的になっている。
次に株式市場への影響を見よう。以下の図は、1925年から2007年にかけての時期におけるダウ平均株価(Dow Jones Industrial Average)の11年移動平均との偏差と太陽黒点数の変動とを重ね合わせたものである。
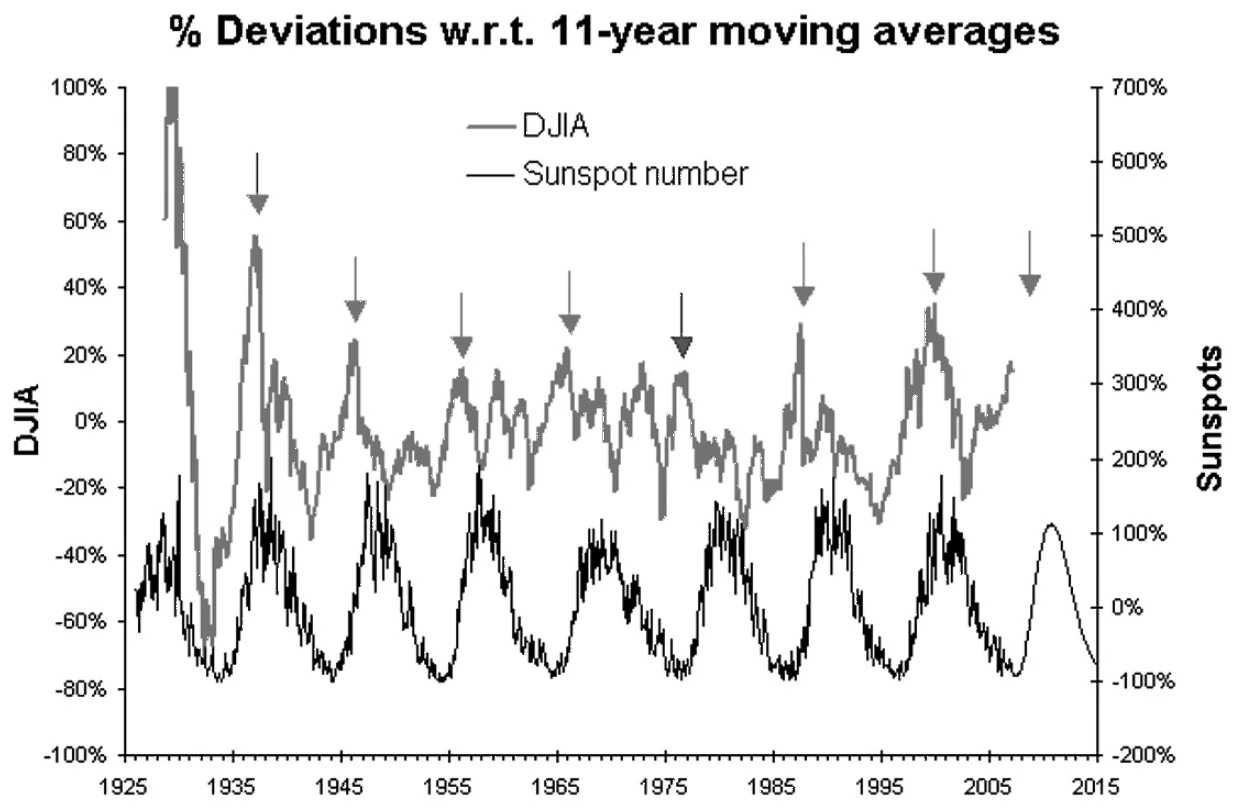
矢印だけを見ると、シュワーベ周期の極大期と対応しているように見える。しかし、ダウ平均株価上昇率にはそれ以外にも小さなピークがあり、対応関係は明瞭ではない。それでも2007年5月に提出されたこの論文は、これまでの規則性から、ダウ平均株価上昇率と経済成長率が2008年6月にピークに達すると予測した。実際のピークはそれよりも早かったのだが、2008年9月15日に、リーマン・ブラザーズ・ホールディングスが経営破綻し、「リーマン・ショック」と呼ばれる世界金融危機が始まったことで、モディスの「太陽黒点、GDP、株式市場」は、彼が書いた論文の中では最も引用された注目の論文となった。
もとよりこの「予測の的中」は、予測の二重の間違いからたまたまそうなっただけのことで、モディスにとっては誇るべき成果ではなかった。もう一度、上の図17と図18を見られたい。これらの図では、第24サイクルにおける極大期は、2010年末になると予想されていたが、実際には、極小期が予想外に長引いたことにより、2014年の4月になった。そして、ダウ平均株価上昇率と経済成長率のピークは、これまでのように極大期の少し前ではなくて、極小期に出現した。リーマン・ショック後の不況は、これまでのリセッション(景気後退)とはかなり異なるタイミングで起きたのだから、予測が当たったように見えるのは、偶然によるものだったのだ。
モディスが米国経済で発見した一般的傾向は、他の国の経済変動でも確認されている。2015年に、IMFのシニア・エコノミスト、ミハイル・ゴルバネフ(Mikhail Gorbanev)は、先進諸国のリセッションの開始時期と太陽活動の変動との関係を調べた論文を発表した。以下の図は、1962年から2013年にかけてのOECD諸国における景気先行指数と太陽活動の25カ月移動平均線を重ね合わせたものである。太陽黒点数の極大期より少し前に景気先行指数はピークに達し、極大期からしばらくしてから赤色の矢印で示した谷が現れる。
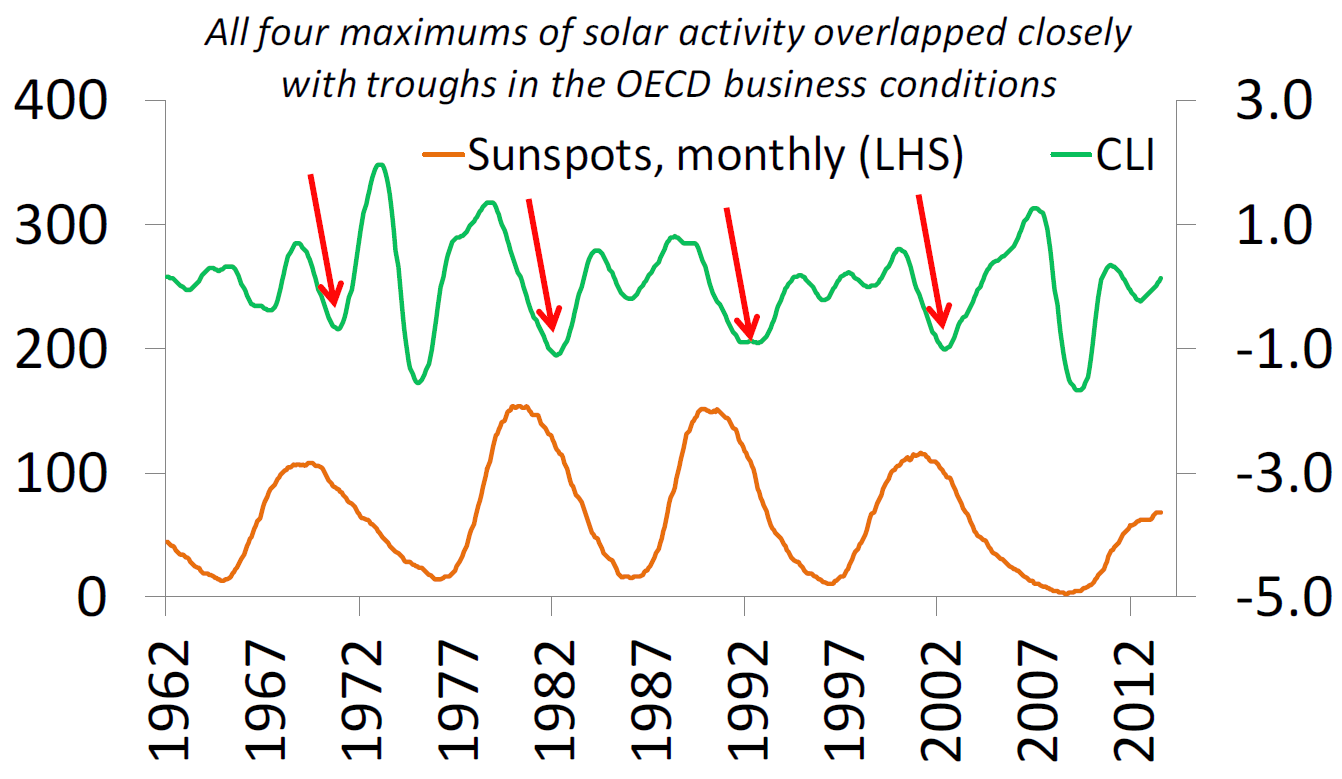
太陽黒点数の変動を24カ月遅らせると、OECDの景気先行指数との間に有意(P<0.0001)な負の相関性(-0.18)が得られる。OECDにBRICsなど新興国六か国の景気先行指数を加えると、相関性は、-0.20となる。このことは、太陽黒点数の極大期から2年経過すると、景気先行指数が底を打つ傾向があるということである。
実際のリセッションは、景気先行指数の低下よりも遅れてやってくる。以下の図は、1965年から2014年までの太陽活動とG7諸国のリセッションの関係を示したものである。縦軸の目盛の3.0は、対応する時期に平均すると7か国中3か国がリセッションに陥っているという意味である。横軸の0は、太陽黒点数が極大になっている時点である。太陽黒点数の周期の第20サイクルから第23サイクルまでの平均値は、青線で描かれている。これまで1年後から3年後にリセッションに陥っていることが多かったということである。
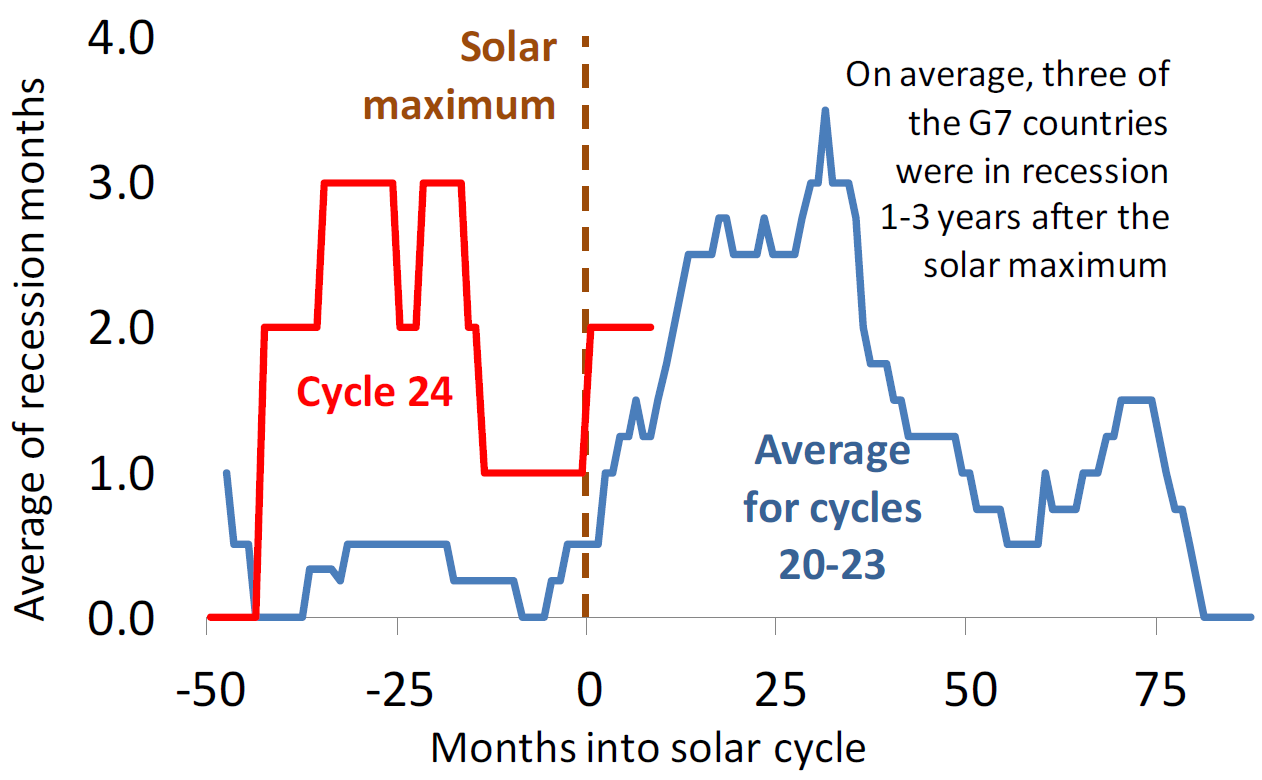
青線のグラフを見ると、極大期の1年後から3年後にある大きな山とは別に、その前後に小さな山があることに気が付く。景気循環論では、一回のジュグラー循環に約40ヶ月を周期とするキチン循環が三回現れると言われている。キチン循環は、英国の経済学者ジョセフ・キチン(Joseph Kitchin, 1861年 – 1932年) が1923年の論文で提案した在庫循環で、他の二つの山はキチン循環で説明できそうだ。
ここでもう一度図20を見られたい。赤い矢印で示された谷は、極大期から1年後から3年後に現れるリセッションに対応している。しかし、緑色の曲線は、その後、極小期のあたりでもう一度谷を形成している。1973年の石油危機、1987年のブラック・マンデー、1997年のアジア通貨危機、1998年のロシア財政危機、2008年のリーマン破綻による世界金融危機といったイベントが発生し、谷間を形成している。
ゴルバネフは、2015年2月に執筆した論文で、第24サイクルにおける極大期が2014年4月であったことをふまえ、2015年の終わりにはリセッションが始まるリスクが高まると予測したが、この予測は外れた。2015年の後半から2016年の春までチャイナ・ショックと呼ばれている中国発の世界同時株安が起きたが、それは実体経済のリセッションをもたらさなかった。なぜ過去の経験則が今回当てはまらなかったのだろうか。
現在進行中の第24サイクルにおける経済は、これまでとは異なるところがある。2007年末から2009年にかけての極小期で起きたサブプライム住宅ローン危機とリーマン破綻による世界金融危機は、期間こそ長くはなかったものの、衝撃の大きさは百年に一度と言われるぐらいで、デフレを回避するべく、日米欧の中央銀行は大規模な量的金融緩和を長期にわたって行った。おそらく、そのため、本来なら2015年から始まるはずのリセッションが先延ばしになったのだろう。
特に2017年に就任したトランプ大統領は、大型減税や公共投資の増額といった本来不況期に行うべき政策を好況期に行った結果、日米では戦後最長の景気拡大が続いている。しかし、景気拡大がいつまでも続くことはない。2007年末~2009年の期間から11年経過した2018年末~2020年の期間は、太陽黒点数との関係で状況が似ているので、要注意である。
3.2. 太陽活動とコンドラチェフ循環との関係
ジュグラー循環よりも長期の景気循環として、クズネッツ循環(Kuznets cycle)とコンドラチェフ循環(Kondratieff cycle)がある。それぞれ、太陽黒点数のヘール周期と短期のグライスベルグ周期(吉村周期)に対応しているが、社会科学の分野でより重要なのは、コンドラチェフ循環である。コンドラチェフ循環は、約55年を周期とする、物価と金利のサイクルで、5回のジュグラー循環から成り立っている。ロシアの経済学者ニコライ・コンドラチエフ(Никола́й Кондра́тьев, 1892年 – 1938年)がその存在を主張したことから、そう呼ばれるようになった。
以下の図の黒色の線は、世界の一人当たり年間エネルギー消費量がS字トレンドからどれだけ偏差しているかを経年グラフにしたものである。 広い灰色の帯は56年周期の正弦波で、これと正の相関(0.72)がある。
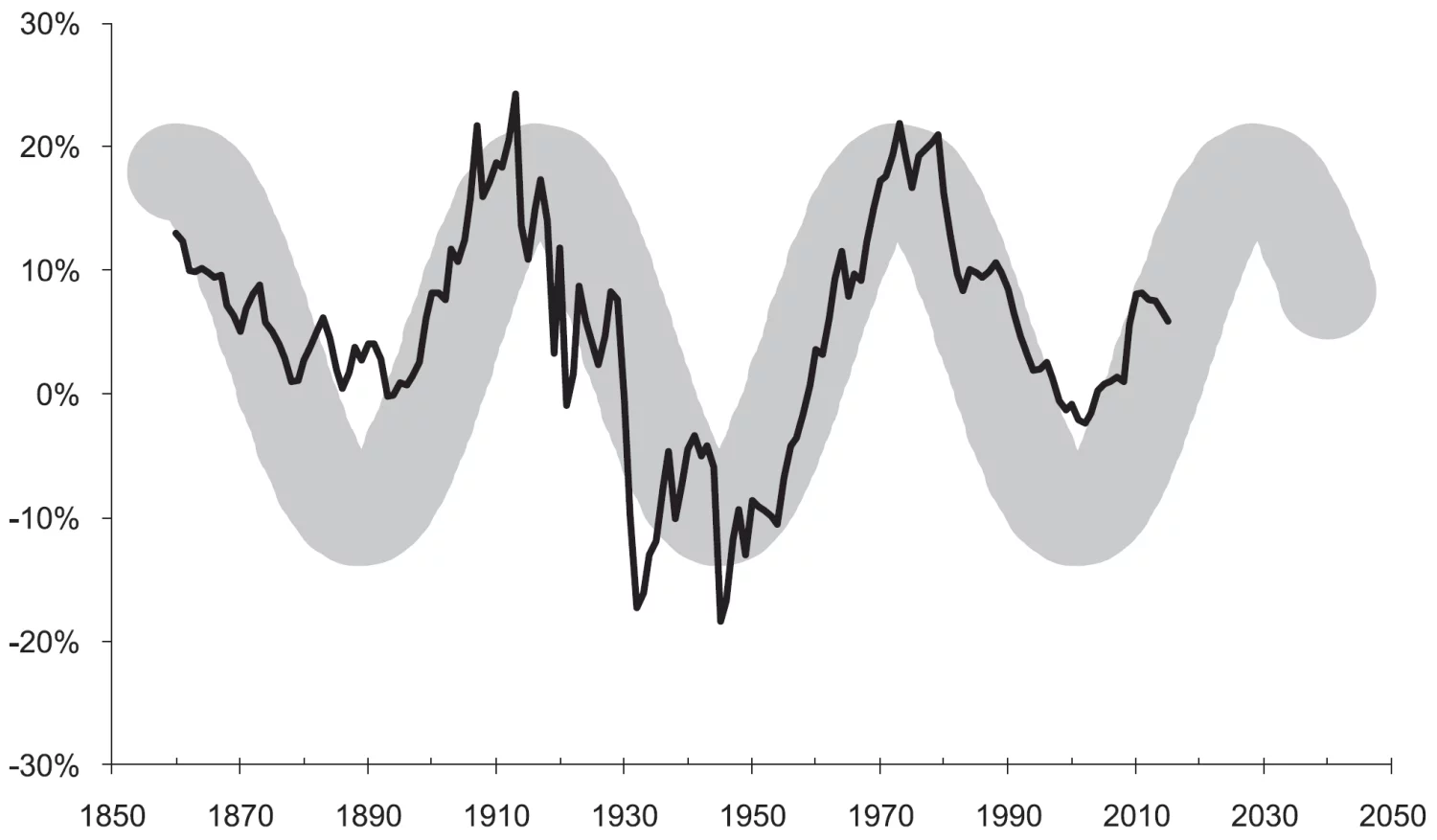
一般的な物価変動の波は、これよりももっと前からある。以下の図の黒色の線は、1590年から2014年にかけて英国の卸売物価指数を55年移動平均を基準にして27年間で平滑化したグラフである。灰色の波は、55.8年を周期とした正弦波で、理想化されたモデルと比べると不規則だが、星印(*)に着目すると、ほぼ55年ごとに物価が上下していることがわかる。物価が上昇すれば名目金利も上昇するので、物価の波動は金利の波動でもある。
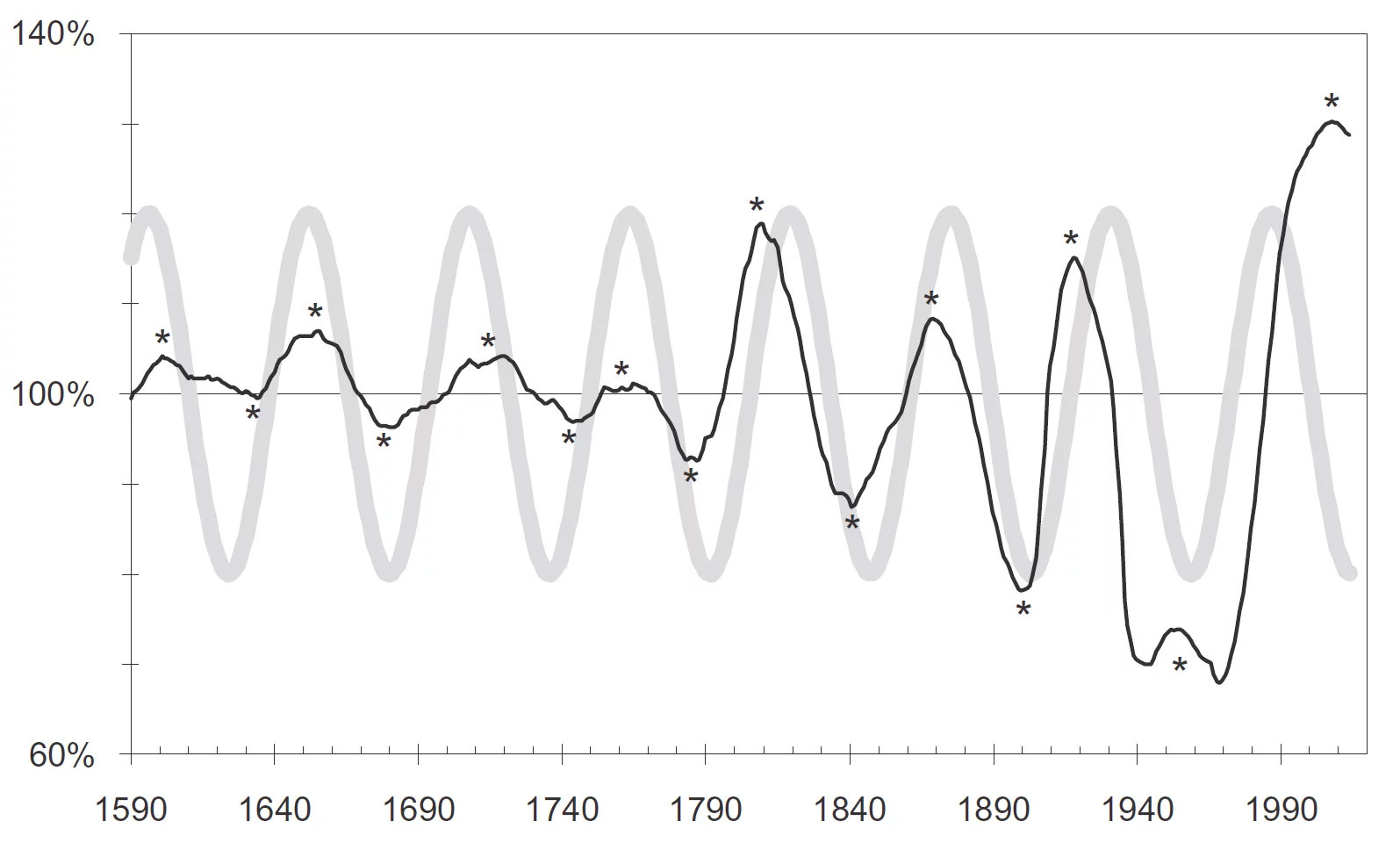
このグラフからわかるもう一つのことは、英国で産業革命が起きた18世紀の末から振幅が大きくなっていることである。産業革命による生産力の増大それ自体は物価を押し下げる要因である。しかし生産力の増大は同時に人口爆発による経済の拡大をもたらし、それは物価を押し上げる要因になっている。コンドラチェフ循環では、産業革命以降の波動は特に重視され、以下の表にまとめたように、各波動に通し番号がつけられている。
| 通番 | 谷底 | 頂点 | 谷底 |
|---|---|---|---|
| 第一波 | 1789-1793年 | 1810-1817年 | 1844-1851年 |
| 第二波 | 1844-1851年 | 1870-1875年 | 1890-1896年 |
| 第三波 | 1890-1896年 | 1914-1920年 | 1939-1950年 |
| 第四波 | 1939-1950年 | 1968-1974年 | 1984-1991年 |
| 第五波 | 1984-1991年 | 2008-2010年 | 2045年頃? |
今日の経済学者は、コンドラチェフ循環は技術革新によって起きると考えている。技術革新によって新しい産業が生まれると、経済は成長し、インフレになる。これが波動の上昇局面である。しかし技術革新が一巡すると、経済成長は低迷し、デフレになる。これが波動の下落局面である。しかし、この下落局面において、次の技術革新につながる重要な科学的発明や技術的ブレイクスルーがあり、次の上昇局面で普及していく。技術革新による新産業とは、第一波では、蒸気機関を使った繊維産業、第二波では、製鉄業と鉄道産業、第三波では、電気産業と化学産業、第四波では、自動車産業、航空産業、石油化学産業、そして現代の第五波では、情報産業やバイオ産業である。第五波が終わるのは、2045年頃という計算になる。カーツワイルがシンギュラリティと位置付ける年である。それ以降に起きる第六波は、人工知能が主導する新産業ということになりそうだ。
経済学者は、他の専門家たちが自分たちの専門分野に対してそうするように、経済を独立した分野として扱いたがるものだ。しかし、私はコンドラチェフ循環を経済システムに内在する自律的な循環とは認識しない。既に述べたとおり、地球の気候には、50~70年周期の気候レジーム・シフトのサイクルがある。ここで図6を見直してみよう。バンドパス・フィルターをかけた北太平洋指数(緑色のグラフ)の谷底と頂点が、コンドラチェフ循環のそれとほぼ一致している。レジーム・シフトを日本語に訳すと、体制交代といったところだが、それはたんに気候の体制を交代させるだけでなく、経済や政治など社会システムの体制をも交代させる。
コンドラチェフ循環の上昇局面では、戦争が頻発し、それが物価を上昇させる。そして頂点で国際政治のレジームが確立する。第一波動の上昇局面は、英国がフランスとの覇権争いに勝利した時期で、1789年のフランス革命に始まって1815年のナポレオン戦争の終結で終わる。第二波動の上昇局面は、プロイセン王国(後のドイツ帝国)が普墺戦争や普仏戦争を経てヨーロッパ大陸の覇者として台頭し、ビスマルク体制が確立した時期である。第三波動の上昇局面は、英国がドイツとの覇権争いに勝利した時期で、1918年の第一次世界大戦の終結で終わる。第四波動の上昇局面は、米国の覇権に最初は日独伊の枢軸国が、次にソ連を中心とした社会主義諸国が挑んだ期間で、ベトナム戦争が終わるまで、戦争が相次いだ。上昇局面で確立した冷戦体制は、その後の下落局面で、社会主義陣営の自壊という形で終わった。第五波動の上昇局面は、米国とイスラム文明との「文明の衝突」として特徴づけられ、1991年の湾岸戦争から始まって2010年のイラク戦争の終結で終わる。
太陽黒点数との関係では、コンドラチェフ循環は逆相関となる。すなわち、太陽黒点数が長期的に減少するときは、気候が悪化し、資源不足からインフレになりやすいため、コンドラチェフの波動は上昇局面となる。逆に太陽黒点数が長期的に増加するときは、気候が好転し、資源が豊富となってデフレになりやすいため、コンドラチェフの波動は下降局面となる。11周期の極大期で革命が起きやすいことは既に述べたが、55年周期でも同じで、太陽活動が活発なコンドラチェフ循環の谷間では、激しい磁気嵐のおかげで人々は冷静な判断力を失い、戦争を起こしやすくなると考えることができる。
太陽活動の55年周期は、19世紀後半には既にルドルフ・ウォルフ(Rudolf Wolf, 1816年 – 1893年)によって提案されていたらしいが、日本では、吉村宏和がその存在を主張したことから、吉村周期とも呼ばれている。吉村は、1979年の論文で、シュワーベ周期を以下の図のようにグルーピングできると主張している。

このグラフを見ると、(Ⅳ)と記された吉村周期だけが、明確な山を形成していないことがわかる。これは、吉村周期よりももっと長期の周期であるドフリース周期(シュース周期)の谷間にあたるからである。
1
トラックバック
このエントリーのトラックバックURL:
http://blog.sizen-kankyo.com/blog/2020/01/4523.html/trackback
