asaokaです。 (前半から間があいてしまいました  )
)
前回の前半 [1]で、誰もが感じる経験則の『暖かさ』から、普遍的な評価指標値として法則化した『温度』が創出され、その温度から『熱』の概念・基本法則が生まれたことがわかりました。
さらにここから、熱の“量”の概念化・法則化が創出され、万物の活動・関係の理解が進んでいきます。

画像は「才野敏郎氏サイト:地球の熱収支」 [2]より引用させて頂きました。
[ブログランキングに参加しています。続きを読む前に↓クリックお願いします]
『「熱学外論 槌田 敦 著」より引用
■熱量の測定
物体に熱qを注入すると物体の温度Tが上がる。 これは次の式として表わせる。
mcΔT=q ・・・・(1.2)
ここでΔ(デルタ)は変化高を示す記号である。また、mは物体の質量、cは比熱で、mcは熱容量と呼ばれている。
熱量の単位としては、純水の水1gの温度を1℃引き上げるのに必要な熱量とし、これを1カロリーと定める。この定義から、水の比熱は、c=1cal/g・degということになる。
その他の物体の比熱は、水との比較で求めればよい。
世の中の物質で最も大きい比熱をもっているのは水である。
水はきわめて特異な物質で、比熱が大きい以外に、融解熱も蒸発熱も大きいなどいろいろある。
物体の温度を上げる方法としては、熱を加えることのほかに、この物体に力学的または電気的に仕事wを加えても良い。 そこで、
mcΔT=q+w ・・・・(1.3) と書くことが出来る。
しかし、熱と仕事はまったく同じものというわけにはいかない。熱をすべて仕事に変えることはできない。
熱はエントロピーをもつ流れであり、仕事はエントロピーをもたないエネルギーの流れであって、まったく同じものというわけにはいかないからである。
ここで述べている水の特性は、「エントロピーから自然の循環」を考えるうえでとても重要です。
あと、物体の熱を上げる方法は、ダイレクトに熱を加えることと、仕事を加える方法があることがありますが、仕事を加える場合は全てが熱に変わるわけではないという点もとても重要ですね 😮
■物体の熱エネルギー
物体に熱qや仕事wを加えたり減らしたりして、その物体の温度Tを変化させたとき、加減した熱などのエネルギーは、物体の中に固定された「熱エネルギーU」になると考えるのが合理的である。そこで、この変化高をΔUとすれば、
ΔU=q+w ・・・・(1.5) と書くことが出来る。
このようにして、物体の中に固定された熱エネルギーがΔUだけ増減した結果、物体の温度が増減ΔTしたり、相変化したりするとして説明するのである。
物体に相変化もなく、ΔUも小さければ、
ΔU=mcΔT ・・・・(1.6) となる。
この物体の状態を示す量Uを近代熱力学の教科書では「内部エネルギー」と呼んでいる。本書では、「熱エネルギー」または「物体に固定された熱」という呼び方をする。
「内部エネルギー=物体に固定された熱」というのはわかりやすいですね。
ここまでの法則式により、『熱』が量として測定可能となりました。つまり、誰もが共通して理解できる評価数値になったのですね。
さて、地球上での熱循環の熱輸送は、大気、海洋、水蒸気などで行われますが、個体や液体と違って、気体は温度や圧力が変わると物体の状態が大きく変化することになるので、大気は大きな要素を占めます。
この大気の活動によって地球上の余分のエントロピーは処分され、生命が存在できるので、ここまでの『物と熱の関係』とともに気体の熱的性質が重要になります。
ここから気体の熱的性質に入っていきましょう。
■気体の熱的性質
①等容加熱
体積を変えないで加熱する場合である。
圧力と温度が変化するが、この変化を、気体の圧力P、体積Vで示すと、
1モルの気体に体積一定で熱qを加えると、その熱エネルギーはΔUだけ変化し、温度はΔTだけ変化する。この1モルの気体を用いるときにはその定積比熱Cvとして、
ΔU=Cv・ΔT=q ・・・・(1.7) となる。
②等圧加熱
圧力一定で加熱すると体積と温度が変化する。
このとき、体積が膨張し、外圧に対して仕事をすることになるので、加えた熱の一部はこの仕事に使われる。そこで、等容加熱した場合と同じ温度になるまでに加える熱量は余計に必要になる。
この膨張で使われる仕事の大きさはPΔVであるが、圧力が一定なのでPV=RTによって、RΔTに等しいのがわかる。
理想気体の場合には、熱(内部)エネルギーUは、温度だけで決まり、圧力や体積に関係ないから、
ΔU=Cv・ΔT=q - RΔT ・・・・(1.8) となる。
この式を書き直すと、
(Cv + R)・ΔT=q ・・・・(1.9) が得られる。 このCv+Rは、等圧変化の低圧比熱Cpである。
③等温膨張
次に、理想気体に熱qを加えながら、等温的に膨張させてみる。このとき、理想気体なので、この気体の熱エネルギーUは変化しない。したがって、式(1.5)によって、
q+w=0 ・・・・(1.10) が得られる。
この式によって気体の等温膨張では、熱が入るとまったく同じ量だけ、仕事が出て行くことが示される。逆に、気体を等温的に圧縮して仕事を加えると、この気体からまったく同じ量の熱が出て行くことになる。これは理想気体の重要な性質である。
④断熱膨張
今度は、熱を加えたり減らしたりしないで、気体を圧縮したり膨張させたりする。
圧縮すると、仕事wが気体の中に入るので、式(1.5)によって、気体の熱エネルギーUが増大する。
逆に膨張させると熱エネルギーは減少する。
ΔU=W ・・・・(1.12)
気体の熱エネルギーが増加すると、式(1.6)によって、気体の温度(T)が上がることになる。
mcΔT=ΔU=W ・・・・(1.13)
これを断熱圧縮による温度上昇といっている。
逆に膨張させると、期待の温度は下がる。この気体の性質は、気象現象で重要である。
以上、経験則『暖かさ』から、普遍的な評価指標値として法則化した『温度』、そしてその温度現象を説明する観念として『熱』理論が生まれ、さらに『熱量』により誰もが熱を評価指標値として認識できるように観念化した。
『熱』という観念の創造は、万物の自然現象の活動・つながりを科学的に説明し、誰もが事実として理解できるように進めたんですね。
そして、この熱理論の延長上にエントロピーがあるのです。
さて、最後に、前回の冒頭で言った(覚えていますよね ![]() )『フェーン現象(山岳の風上側よりも風下側の方が気温が高く乾いた風が吹いてくる現象)』、をここまでの概念で説明してみましょう。
)『フェーン現象(山岳の風上側よりも風下側の方が気温が高く乾いた風が吹いてくる現象)』、をここまでの概念で説明してみましょう。
【フェーン現象とは?】
暖かい季節に南側の海から水蒸気をたくさん含んだ風が陸に上がり山岳を越えてくるとき、山にぶつかった風は上昇気流になる。
そのとき大気の重力の関係で山の上ほど気圧が下がっているので『④断熱膨張』により温度が下がる。
通常100m上昇するごとに1℃温度が下がる。
(山に登ると涼しくなるのは、この気圧低下による温度低下のためなんですね 🙂 )
しかし、このフェーン現象を起こす海からくる風は大量の湿気を含んでいるので、冷やされた空気が水滴になって放熱するためこの風の温度はあまり下がらない。『③等温膨張』+『相変異による潜熱効果』
100m上昇しても0.5℃の温度低下になる。 そして、この水滴は雨となって取り除かれる。
(山は雨が降りやすいのはこのためなんですね 🙂 )
そして、山岳を越えて下降すると再び気圧が上がるので、温度は『④断熱圧縮』で上がる。
このときは風の湿気が雨で取られ温度上昇を緩和する結露機構がないので、100m下がるごとに1℃の温度上昇を起こし、山岳を越える前に比べて温度は高くなる。
例えば、気温20℃、相対湿度60%の風が、2,000mの山岳にぶつかった場合、
風は約1,000mの地点で10℃になり露点に達する。
そのまま結露と温度低下を起こしながら上昇するので風は頂上で約5℃になり、
山を下りる時は結露を起こさず温度上昇だけを起こすので風は地上で約25℃+30%ほどになり、
山岳の風上側より風下側の方が高温で乾いた風になる。
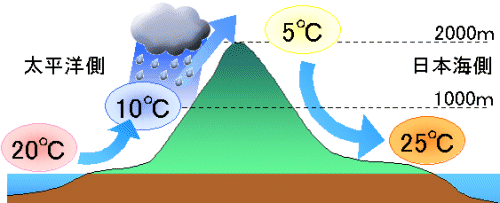
画像はここから [3]引用させて頂きました。
できました!? 😀
長いのに最後まで読んでくれてありがとう。
次回は、エントロピーに入っていく予定です。